In part 2 of this series we used chromatic circle diagrams to show how chords and scales are affected by chromatic inversion – the basic operation of negative or mirror harmony. We noted that there are twelve available reflection points or ‘axes’.
Jacob Collier popularised the use of one specific axis, located 3½ semitones above the tonic. This axis reflects a major key into its parallel minor. If used selectively within a piece, this will have the effect of borrowing some harmony from the parallel minor – an example of the process known as modal interchange.
Other axes will introduce negative harmony from other keys. One could, for example, reflect a major key into its relative minor, using an axis a whole tone above the tonic. Other, more distant keys can also be reached.
The harmonic vocabulary of jazz is based on four-note chords. As a basic negative-harmony kit for jazz musicians, here are six of the seven diatonic chords of a major key, with their mirror chords in the corresponding minor key. There remains one ‘awkward’ chord in each key, which we will come to shortly. We shall use the ‘Collier’ axis to start with.
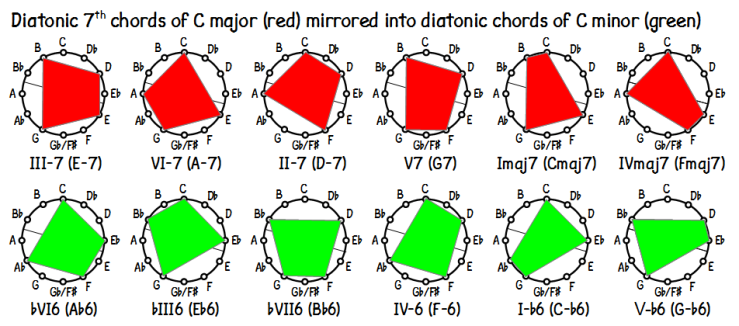
All the sixth chords have alternative spellings as seventh chords. For example IV-6 has the same tones as I-7b5. However, consistently reflecting seventh chords into sixth chords ensures the root movement in the original key is accurately reflected.
The chords are shown in cadential order, with roots moving upward in fifths or, after reflection, downward in fifths. However, you won’t often find a progression built entirely from these diatonic chords. Most times, secondary dominants and other non-diatonic chords are introduced. Secondary dominants, like the primary dominant, will be represented by minor sixth chords in the reflected progression.
For the sake of completeness, here is the mapping between sixth chords in the major key and seventh chords in the minor key.
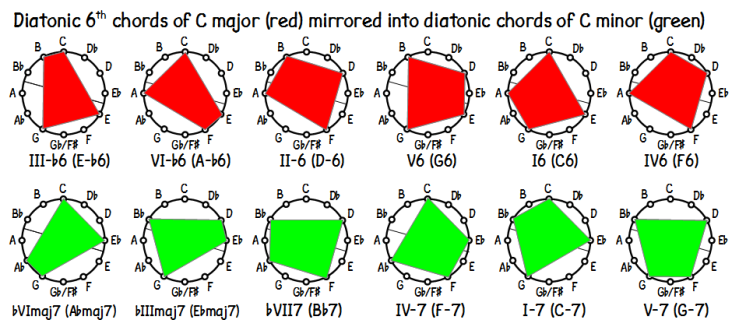
This chart, like the previous one, could in principle be used in either direction: from major to minor, or minor to major. However, I will not pretend that these charts are all that useful for creating negative versions of passages in minor keys. They only show tones and chords drawn from the aeolian mode or ‘natural’ minor. Real minor harmony makes extensive use of non-aeolian scale tones such as the major 6th and 7th. The V chord in the common minor cadence, II-7b5, V7b9, I-7 includes the harmonic minor’s sharpened leading note. And look, there’s that awkward II-7b5 chord, which I did not even include in the charts.
Reflection is a symmetric process. So why should it be more difficult in one direction than in the other? The asymmetry is between the way we make music in major keys, and the way we make it in minor keys. Minor music constantly wanders outside the diatonic pitch class set. In less technical language: you could easily write a piece in C major using only the white keys on the piano; but a piece in A minor will almost inevitably use the black keys also.
We now have three reasons why music might acquire a different, unusual sound when reflected into negative harmony:
- root movement: rising fifths are replaced by descending fifths
- sixth chords: jazz usually contains more 7th chords than 6th chords; reflection reverses the balance, producing many 6th chords
- chromaticism: major harmony created by reflection may sound more chromatic than expected, and minor harmony less chromatic than expected
The first two points are intimately connected: if we choose to reflect the root movement accurately, seventh chords must become sixth chords, and vice versa. The third effect, on chromaticism, will only be noticeable if musicians stick rigorously to the reflection formula and make no further note or chord substitutions.
Root movement
In my previous post I gave a rather fussy rule for finding the root of a reflected chord. But there is a simpler one. Whatever axis we used to reflect the chord, it turns out that we can reflect roots in the same way, just using a different axis. The axis for roots is always 3½ semitones below the main axis, or 3½ notches anticlockwise of it on the chromatic circle. Essentially this means you can reflect basslines in the same way as you reflect melodies or chords. You just have to hold the mirror in a slightly different place.
It’s quite simple really. If you shift the axis downward by 3½ semitones, anything reflected in the axis will be shifted down by twice that distance, which is a perfect fifth. This means that the root of a triad will reflect into the root, rather than the fifth, of another triad. Which is what you’d probably want.

The ‘awkward’ chord in C major is the VII chord, B-7b5. Reflection in the Eb/E axis gives us the mirror chord F, D, Ab, Bb which you would probably spell as Bb7. Reflecting the root, B, in the C axis gives us Db. So our rule offers us a root which is not any of the notes of the mirror chord. It is not even a note in the C minor scale.
Something similar happens when we try to reflect the II chord of C minor, which is D-7b5. Our rules offer us an F7 chord with, incongruously, Bb as its root.
It is always the chord with a flat fifth that causes the problem. To provide a root for a reflected chord, we need a perfect fifth in the original chord.
The relatively painless solution is to re-spell the semi-diminished chords as minor sixth chords. In C major, this means re-spelling B-7b5 as D-6. This reflects uneventfully into Bb7, which is a diatonic chord of the mirror key, C minor. I am sure musicians will find other ways around the problem – if they even see it as a problem.
Other keys
So far, we have been using the ‘Collier’ axis which flips harmony between parallel major and minor keys. What happens if we use a different axis, which bounces the harmony into some other key? Thanks to the magic of symmetry, all the mirrored notes, chords, scales and roots will remain in the same relationships, simply transposed into the new key. The Roman numeral symbols for chords in the mirror key will still be valid.

If you intend to combine ‘positive’ elements in the original key with ‘negative’ material in the new key, the choice of axis is an important decision. I think this is where the interesting possibilities lie. On the other hand, if you simply want to turn a whole piece upside-down and hear how it sounds, your choice of axis is simply a choice of the key you want to play in.
I hope some musicians will experiment with the eleven neglected varieties of mirror harmony. Some of them may seem pretty wild. But then, jazz musicians are masters of modulating to distant keys and making it sound convincing.
What’s Levy got to do with it?
Many people assume that the reflection axis mentioned by Jacob Collier, in those few seconds of off-the-cuff video, comes straight out of a book by the twentieth-century Swiss composer Ernst Levy, called A Theory of Harmony. It doesn’t.
(Here is the video, if you still haven’t seen it.)
The idea of reflecting triads was important to Levy. It’s how he accounts for the very existence of minor triads. Early in the book he shows how a C major triad, reflected in the tonic C, produces an F minor triad. On our chart of the twelve ways of reflecting a C major triad, this corresponds to the last example in the top row. The axis that Collier mentions, which reflects C major into C minor, is the first in the top row.
But one idea in Collier’s video has obvious echoes of Levy. It is the idea that a progression of minor triads, rising in fifths, has the same dynamic as a sequence of major triads descending in fifths. Here is the relevant diagram from Levy’s book, and my attempt at a reinterpretation.
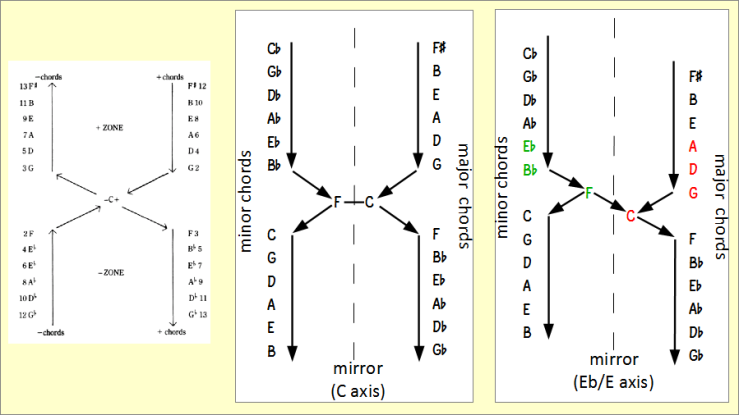
Here is how Levy describes his diagram:
“C is at the intersection of four roads. Normally, one should use two of them to proceed towards C; the two others, to get away from C. That provides two normal ‘falling’ cadence chains, and two cadence chains in contrary motion giving the impression not of a fall but of an expenditure of energy to keep up the motion.”
I don’t always agree with the way Levy hears things, but that ‘expenditure of energy’ is exactly what I felt, two posts back, from that Joss Stone track where the harmony climbs in fifths from C7 through G7, D7, A7 to E7. Allowing for the different key, that is a climb up the bottom right-hand branch of Levy’s diagram.
See if you get the same uphill feeling from Jimi Hendrix at the start of Hey Joe.
Levy’s diagram can be confusing, so I have changed a few things in my version.
- Levy names triads by their ‘generators’ rather than their conventional roots. C+ is a C major triad (CEG). Its reflection (FAbC) has the same generator (C) so Levy calls it C-. I have given it its conventional name of F minor, and similarly renamed all the other minor chords.
- At the centre of the diagram, where Levy writes “-C+” to emphasise the close equivalence of these two chords, I have separated the F minor and C major triads for greater clarity.
- I have swapped the upper and lower branches on the left (negative) side of the diagram, so as to make gravity work consistently in a downward direction.
- This places each negative chord opposite its positive counterpart. I have added a ‘mirror’ line to emphasise this relationship.
In the third diagram the ‘major’ side has been moved down one notch, to emphasise the symmetry between two progressions towards C major: on the right, A, D, G, C; and on the left, Eb-, Bb-, F-, C. Embellished with sevenths and sixths, these progressions are the examples in Jacob Collier’s video (at 3m17s). The approach from the minor side is the one that Collier describes as “epic, warm and wonderful”.
In the third diagram, chords are looking at new counterparts in the mirror: C major and C minor, for example, are now mirror buddies. The axis – the mirror point – is now that famous location, the crack between Eb and E.
I want to stress that this particular axis only emerges after Levy’s diagram has been seriously hacked about, in ways that Levy might not have welcomed. I don’t think Jacob Collier went through any of this thought process. He probably just said ‘that’s where the axis should be’ in a flash of his laser-like musical intuition.
It’s a great axis to choose (quite possibly the only choice) if
- you want to approach a chord in two ways, one from the major and one from the minor side
- the target chord, whether major or minor, will be the same, whichever approach chords are used
- the harmony must move in fifths: either upwards or downwards, but strictly in fifths
- the harmony should not go ‘uphill’ according to Levy’s definition of gravity
I shall use my last few paragraphs to suggest why jazz musicians in 2017 should respect Ernest Levy, but not waste too much time on him.

Levy’s book offers a theory of existing harmonic practice. In contrast to George Russell or Olivier Messiaen, Levy was not an evangelist for new compositional techniques. He was fascinated by Pythagorean number mysticism, and announced his intention “to develop a harmonic theory not from natural phenomena but from spiritual principles”.
Paradoxically, he based his theory on the overtone series – the harmonics or upper partials that can be sounded on a string or a pipe – and then had to explain how this natural phenomenon just happens to follow the mathematics of our inner sense of proportion.
As Levy must soon have realised, this disregard for the physical world, and insistence on spiritual absolutes, makes music theory very difficult and inflexible. Poor old Pythagoras cannot be expected to explain everything that happened in music during the next 2000 years. Levy never really engaged with jazz, either through lack of interest, or possibly because he knew jazz would blow his theory out of the water.
Levy was not a fool. I think he knew his project was not going well. He did not throw his manuscript in the fire, but he let it gather dust for 40 years. We should probably be grateful to Siegmund Levarie for editing and publishing the book after Levy’s death, even though (another 36 years on) it reads as a record of a worthy but unsuccessful intellectual foray.
Music theory has moved on. Other approaches have been more productive. But if musicians can salvage a few fragments of Levy’s work and turn them to creative use, I guess that is something to celebrate.


[…] the b3/3 axis, then select the root note by reflecting the original root across the tonic (1) axis. Part 3 of Jazzmodes’ negative harmony series has some more explanation on why it makes sense to select the root this way. In short, it’s […]
LikeLike
Tony, your first revision of Levy’s chart (center one on this page) certainly makes it easier to follow Levy’s ideas. I don’t worry at all about the absence of undertones in nature (since background is physics I appreciate the analogy with imaginary numbers), but after pondering over the polarity theory (for years) it seems to break down when it comes to cadences. Staying on the right (major) side, all is well: following the arrows, you depart from C (tonic) to F (subdominant), cross over to G (dominant), then “fall” back to C. Not so on the negative side: it has you depart from F_m (tonic) to C_m (dominant!), cross over to B-flat_m (subdominant!), then “fall” back to C_m. This gives a plagal cadence instead of the stronger authentic cadence, and my ear simply does not hear them as equivalent in the way suggested by Levy. My solution (which I haven’t seen elsewhere in the context of polarity) is another inversion: time. If, in minor keys, you reverse the order in which chords are played, you get tonic – subdominant – dominant – tonic; that is, you restore the authentic cadence. This suggests reversing the arrows on the negative (minor) side of the chart. So the whole scheme therefore is to invert both the frequency and time relationships to explain minor harmonies (this sort of thing is done all the time in theoretical physics). I have toyed around with this a bit, rewriting well-known songs in major keys, replacing major chords by their “polaric” minors then playing the result backwards, but it is time-consuming. Anyway, I’d love to hear your thoughts about time-inversion.
LikeLike
Typo in earlier post today: the end of fourth sentence should read, “… then “fall” back to F_m.”
LikeLike
Like you, I fail to hear the supposed preference for plagal resolution of minor chords. Sure, you could patch up Levy’s theory, so that it agrees better with your ears. And time-reversal might be one way to do it. But I view this like a builder surveying a rickety old house. You could repair it, but is it worth the effort?
Good luck with your experiments with time-and-pitch-reflected songs. If it sounds good, you can fix the theory later.
LikeLike
very interesting what @Francis von Zuben said about time mirror. In 17th century understanding of the so called Clausulae (Klausellehre in german), which are just melodic cells of two notes, one resolving into the other, there was already the idea that plagal cadences are nothing but a mirrored authentic cadence. You can try this yourself. Play I – IV slowly and then back to I. And then again back to IV. And again back to I. By now you’ll realise there’s a tension again towards IV and so on. It never fully comes to an end.
LikeLike
Thanks tony for your input. I am writing my masters thesis in music theory on the broad topic of polarity, symmetry and negative harmony, trying to combine the two worlds of jazz and classical music, both my home. I’ve spent months reading stuff and at the end I must say, most of jazz bloggers and youtube channels just don’t even try to find out a bit more about Levy’s background. Because if they would, they’d realise that he is just the end of the long tradition of the Harmonic Dualism, that begun in the 19th century with Von Oettingen, Hauptmann or Riemann, and which basically defined major and minor as a reciprocal phenomena. Levy never intended to be a music theorist like the others. He saw himself as a composer, and what he did was bringing the harmonic dualism in its more extreme version, the polarism, together with his own metaphysical ideas and with his pytagoreic approach. The only reason why Levy became such a big thing, is because Coleman read it. Why did Coleman read it? nobody knows, but it has probably something to do with Levy and Levarie being US-Citizens. Levy is just really a cool guy and I like his book, but it is the worst way of getting in touch with the classical theory of harmonic dualism and polarism… So no wonder everybody is having trouble with it.
LikeLike
Although music, like microphysics, is theoretically reversible, the human experience of music is dominated by the arrow of time. The beat goes on! So I have never taken time reversal very seriously in music.
But harmonic progression (in jazz especially) is often about going somewhere and finding a way back. One way back is simply to retrace your steps. There are many tunes with a I-IV-V-IV-I vamp. I think both players and listeners are at least dimly aware that this pattern is symmetrical in time. Melodic lines also get reversed (not always exactly – broken symmetry is more interesting).
So, yes, time reversal is a thing in music.
LikeLike
Fantastic that you are doing a thesis on this. It will be a great service if you can put Levy into context, and place him in the history of dualism, polarism or whatever we call it.
LikeLike
Along the lines of my earlier post, I tested the time-reversal hypothesis on a very simple tune, “Happy Birthday,” with discouraging results. The traditional tune is entirely major, progressing as I-V-I-IV-I-V-I, ending with an authentic cadence. I wrote the original score in the key of C as major triads built on each note of the melody. Then I reversed the order, retaining time values, but replacing each chord with its “mirror image”, forming triads downward a major third and perfect fifth from each note in the reversed melody (thus, each C-major became F-minor, and so on). I picked out the new melody from the roots of these new chords (in Levy’s “telluric gravity” sense – the lowest notes of the triads) and played it on a classical guitar, accompanied by the new harmonies thus created.
The resulting composition in F-minor sounds terrible (to me at least). To begin with, the song ends unconvincingly with two eighth notes rather than a half note. More importantly, the progression i-v-i-iv-i-v-i does not, strictly speaking, contain an authentic cadence. For minor keys, an authentic cadence is given by V-i or the stronger V7-i, requiring notes outside of the natural minor scale.
The problem is that we hear the lowest note of minor triads as their roots despite their being generated from their highest notes (in Levy’s “absolute conception”). This yields the Aeolian rather than the Phrygian mode as the natural minor scale which disrupts the time-frequency symmetry. There is no leading tone on the fifth degree; instead, it appears on the fourth degree, and so is heard in the plagal cadence iv-i. While this can be strengthened to iv6-i using notes within the scale, it lacks the finality of the authentic cadence (to my ears, anyway).
LikeLike