
Last time we surveyed the rich culture that surrounds music’s circle of fifths: the posters, gadgets, apps, clocks and t-shirts, and the almost endless variants of the iconic diagram. But apart from the human fondness for zodiacs, mandalas and other circular things, what are the secrets of its success?
This time I’ll be looking at the origins of the circle of fifths, and some of its musical uses. Next time, a lesser-known but fascinating application of the circle. After that, I’ll look into the theory behind the circle of fifths, why it is so useful, and why it exists at all.
First, let’s sort out the terminology. Circle of fifths, cycle of fifths, circle of fourths?
I try to say ‘circle’ when I mean the diagram, and ‘cycle’ when I am describing a chord progression or referring to the abstract concept behind the diagram. But I often default to ‘circle’.
Fifths or fourths? For my money, circle (or cycle) of fifths is the one, because it is universally used and understood. We do not need two names, or two diagrams. The step between C and G can be read as either a fifth or, in the other direction, a fourth. So the circle of fifths is also a circle of fourths.
Which way is up? The diagram is usually drawn with C at 12 o’clock, E at 3 o’clock, F#/Gb at 6 and Ab at 9. But it can be rotated into any orientation, or reflected in a mirror, and it will still work. You might reasonably draw the diagram differently when you are illustrating the relationships between chords in a key other than C. In an app, this is an easy and natural thing to do.
Origins


The circular stave, adorned with key signatures, vividly conveys the way each key morphs into the next, by changing just one tone at a time. It would be perfect, if only the transition from ‘sharp’ keys to ‘flat’ keys could be handled a bit better.
In the short step from Db to F# major, it looks as though the scale is completely rejigged: five flats are cancelled and six sharps are applied. In fact, of course, only one tone changes: the C in Db major drops to B in F#. The other six tones don’t change pitch. Only their names change. (In modern equal temperament this is exactly true. But even in historic tunings, the pitches are very close.¹)
Could we make this continuity of pitches more obvious? One way would be to interlace the stave with itself, at the point where the circle closes, so that each stave line turns into a space and each space into a line. The 6 o’clock position on the circle would be occupied by two equivalent keys, Gb and F#, and the stave would do something like this (though possibly the other way up):




Circle of fifths diagrams were invented and popularised because the concept of a cycle of fifths was in the air at that time. The old church modes were on the way out, replaced by the new concept of major and minor keys. Musicians had begun to think about a series of transpositions or modulations that would return to its starting point after going through a number of keys.
How many keys? Twelve major, plus twelve minor, seemed to do the trick². And twelve pitches in each octave were sufficient to build twelve seven-note scales, because each pitch could be re-used in several keys.
There were a few tuning glitches, ‘wolf’ intervals and the like. Harpsichord and organ tuners struggled with these issues for years, using both the concept and the diagram of the circle of fifths. I’ll come back to that and other specialised uses later, after considering the circle of fifths in its most familiar guise, as a mnemonic for key signatures.
A key to key signatures
This is quite possibly the diagram’s most important single use. It does the job well, until we reach the more extreme key signatures with six or more accidentals. The closed circle clearly asks us to accept that F# and Gb are the same key. But this is an additional fact that has to be learned. You would never guess it from the way key signatures are written.
There is a bit of a disconnect here. Music is taught on the basis that there are 12 pitches per octave, 12 major keys and 12 minor keys. It’s a closed, finite system. And though keys are clearly different in the way they interact with instruments, voices and ears, all keys are theoretically equivalent and there is certainly no one key that is special.
By naming seven pitches with the letters A to G, and treating all other pitches as modifications of those seven, our notation makes one tonality – C major – look special. C isn’t special. It’s just lucky.
Because all pitches other than A to G must be notated with sharps and flats, we soon encounter pitches where there is a notational choice: A# or Bb? F# or Gb?
In any given context, does it matter whether we write Bb or A#? Yes, but mainly because it is helpful to have some rules to keep written music intelligible. One rule is to use each letter-name (and thus, each stave position) exactly once in each seven-note scale. In an A major scale, we agree to call its third degree C# rather than Db or, lord help us, B##. The idea is to get an alphabetic sequence (A, B, C#, D, E, F#, G#, A) rather than something like A, B, B##, D, E, Gb, G#, A which identifies the correct piano keys but is utterly confusing.
It’s a pain having to learn those notational conventions. Much of what is taught as music theory is really a set of rules for operating in a 12-tone, all-keys-are-equal world, while using a notation which seems to describe a completely different universe. A universe where monks were the musicians, God was the audience, harmony was just a glint in melody’s eye, key-changes didn’t happen, seven stave positions per octave seemed sufficient, and seven names for pitches looked like all we’d ever need. Happy days.
If you can see past the notational fog of sharps and flats, the circle of fifths is telling us something fundamental about Western music. Whatever major scale you start with, you can always sharpen the fourth or flatten the seventh to make another major scale. It is this that allows us to arrange 12 major scales in a circle.
Not all scales have this property. Take a melodic minor scale, for example. There is no way you can alter a single tone and still have a melodic minor scale. I’ll have more to say about the peculiar properties of diatonic scales in a future post.
The circle of fifths as a practice aid
Whether it’s scales, arpeggios, 2-5-1s or Charlie Parker licks, jazz students are always told to practise in all twelve keys. The circle of fifths, as a map of tonalities, provides a systematic way of doing this.
For scales, licks or complete tunes, stepping around the circle either clockwise or anticlockwise can be helpful. Moving in fifths, up or down, ensures that changes in the tonal palette (the key signature, basically) are as gradual as possible. On the piano, your hands will be making shapes which change only gradually as you progress through the keys.
Piano students are often taught to practise 2-5-1s (cadences) in the cycle C, Bb, Ab, Gb, E, D, C. That means moving down by whole steps, equivalent to two fifths at a time. Why? Well, it sounds musical; it minimises hand movement; and it is good preparation for tunes like Victor Young’s Stella By Starlight where 2-5s are chained. Basically this is the route tunes take when they want to get home in a hurry, with no harmonic fuss.
The last line of Stella has the chords E-7b5, A7, D-7b5, G7, C-7b5, F7, Bbmaj7. That’s three chained minor 2-5s, followed by a major resolution. Though only three tonalities (D, C and Bb) are implied, we’ve got seven consecutive chord roots there in circle-of-fifths sequence. Another example: the bridge of Clifford Brown’s Joy Spring contains three complete, major 2-5-1s in the sequence G, F, Eb – part of a six-key cycle that most jazz piano students have practised.
For a full 2-5-1 workout you must include the alternate cycle: G, Eb, Db, B, A, G. It is also wise to practise 2-5-1s and 2-5s moving in half steps – for tunes like Strayhorn and Ellington’s Satin Doll, Benny Golson’s Stablemates and John Coltrane’s Moment’s Notice. In fact you have probably got a book, an app or a teacher telling you to cycle through technical exercises in other patterns such as minor thirds, and in random patterns so you are ready for anything.
Tessitura Pro, from mDecks Music, makes a pretty thorough job of this. The whole app is based on the circle of fifths as a device for visualising and comparing ‘structures’ (scales and chords). Choose a structure, and the app can generate a variety of practice exercises, from simple scales and arpeggios to complex patterns. Be aware that the notes shown on the circle are actual notes, not keys or tonalities. The screenshot shows the five notes which make up the C minor pentatonic scale, and an exercise generated from them.

Harmonic progressions
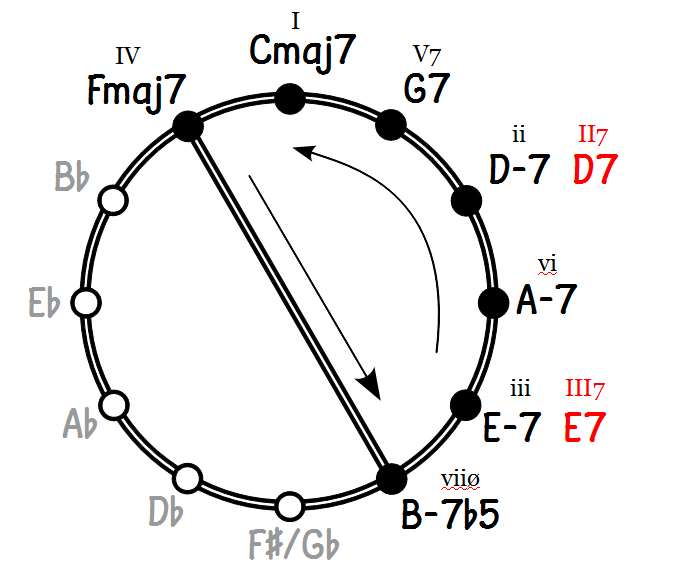
Note that we are no longer using the circle as a chart of tonalities. We are tracking root movement. The diagram above shows how circle-of-fifths progressions operate within a single key, or within a pair of relative major and minor keys. The complete sequence cycles through the full range of diatonic chord qualities. Autumn Leaves, normally regarded as a minor tune, starts with a major cadence (D-7, G7, Cmaj7) before moving into the minor part of the cycle (B-7b5, E7, A-7).
In the B section of the tune, the cadences come in reverse order, minor leading into major, giving the whole section a major feel. It’s just a question of where you start on the loop, and where you finish.
Notice how the chord quality changes progressively during the in-key circle-of-fifths progressions of Autumn Leaves. If you like to think in modes, these progressions go through all seven diatonic modes, from the darkest (locrian) to the brightest (lydian), and then back to locrian.
This contrasts with our earlier examples from Stella by Starlight and Joy Spring, where the tonality changes progressively while the chord qualities (and corresponding modes) follow a simple repetitive pattern. To sum up the differences:
In-key circle of fifths progression
- root movement in descending diatonic fifths – mostly perfect fifths, with one tritone
- confined to a semicircle of the full circle of fifths
- stays within one key, or a relative minor/major pair
- may cycle through all four diatonic, seven-note chord qualities: -7b5, -7 (3 times), 7, maj7 (twice)
- correspondingly cycles through all seven diatonic modes
- on the full cycle, chord quality gets progressively brighter, then darkens again
Through-the-keys circle of fifths progression
- root movement in descending perfect fifths
- potentially covers the entire circle of fifths
- short repeating cycle of chord qualities e.g. (-7, 7), (-7, 7, maj7) or simply (7)
- correspondingly, a short repeating cycle of three or fewer modes
- moves rapidly through keys, adding flats or cancelling sharps
- sense of homecoming or darkening tonality (though this is obviously relative, and no key is intrinsically darker than any other)

In the previous post I mentioned the Chord Wheel, a rotary device based on the circle of fifths. This also exists as an app for iPhones and iPads, with the big bonus of hearing the chords as they would sound on a guitar or piano.
The Chord Wheel is sold as a tool for analysing progressions and creating your own. Its circle-of-fifths layout is ideal for key changes and transpositions. When it comes to exploring chords within a key, you will notice that the seven diatonic chords have been pulled together into a triangular cluster which conceals the fifth relationships between them. Sure, you can tap out the Autumn Leaves sequence, but your finger has to hop around a bit. Perhaps that is no bad thing. If it was too easy to reproduce Autumn Leaves, you might find it correspondingly harder to compose something original.
My next post will describe how the circle of fifths has given 300 years of service in the tuning of keyboard instruments such as the harpsichord, the piano and their electronic successors. It’s a specialised, even geeky subject, but I’ll attempt a not-too-geeky treatment. It will give me a chance to show you some of the most amazing infographics I have come across in the whole field of music.
In the fourth and final article of this series I will investigate why the circle of fifths works, and why it even exists. What is the source of its magic? This leads into deep and still-open questions in music theory. I shall look behind a few doors that most music teachers – very understandably, if you ask me – prefer to leave closed.
Further reading
Each jazz textbook or web resource has its own approach to the subject of circle-of-fifths progressions.
The Berklee Book of Jazz Harmony, by Joe Mulholland and Tom Hojnacki, refers to ‘cycle 5’ progressions. The authors introduce the in-key (diatonic) version in their first chapter, before they have explained minor harmony, so initially they can offer no role for the -7b5 chord. In chapter 2 they introduce the ‘II-V progression’ (major version only) and ‘extended dominant strings’, both of which are examples of through-the-keys cycle-of-fifths progressions.
In Jazzology, Robert Rawlins and Noor Eddine Bahha approach the subject by way of the ii-V-I cadence. They give many examples of in-key and through-the-keys progressions. They cover ‘ii-V chains’ thoroughly, including those which depart from circle-of-fifths root movement. ‘Backcycling dominants’ (chains of dominant 7th chords descending in fifths) are treated separately in the next chapter.
Mark Levine’s Jazz Theory Book states concisely: “You should use the cycle when you practice because it approximates real life. Most chord movement within tunes follows portions of the cycle. For instance the roots of a II-V-I progression follow the cycle.” Chained dominants are introduced as “V of V”. Levine’s book is an easier read than the previous two, because it does not try to fit (force?) everything into the theoretical framework of functional harmony. His survey of other common progressions reminds us that not everything follows the circle of fifths.
The Jazz Piano Site is a useful web resource, with a good page on circle-of-fifths progressions. Three main types are identified.
For details of the the origin of the circle of fifths and the modern key system, an important source is Between Modes and Keys: German Theory, 1592-1802 by Joel Lester.
